개요
전 포스팅에서 비용함수가 최소화될 때 최적의 파라미터를 찾을 수 있다고 서술했었다.
경사하강법은 미분을 이용하여 비용함수가 최소가 되는 지점을 기계가 자동으로 찾아낼 수 있도록 하는 방법이다.
개요는 다음과 같다.
1. 먼저 파라미터를 초기화 한다.
2. J(θ0, θ1)에서 가장 경사진 지점으로 이동한다.
3. 이동한 지점의 θ0, θ1이 새로운 파라미터가 되고, 1,2의 과정을 반복한다.
4. 반복하면 국소 최적(Local Optimum)에 도달한다.이때, 이동의 간격(step)을 지정할 수 있는데 이것을 learning rate, α라고 한다

어떻게 가장 경사진 지점으로 이동할 수 있을까?
그때 사용하는 것이 미분이다. 미분은 어떤 점에서의 기울기를 구할 때 사용한다. 어떤 점에서의 기울기에 비례해서 값을 감소시키면 경사진 지점으로 이동하게 된다. 비용함수에서 하강을 반복하다 보면 어느 순간 비용함수의 최저 지점에 도달할 수 있게 될 것이다.
최저지점에 도달할수록 기울기의 절대값이 작아지고, 하강하는 깊이도 점점 줄어든다. 따라서 비용함수가 일정수준 이상 감소하지 않는 지점을 국소 최적(local optimum)이라 판단하고 학습을 종료한다. 아래는 경사하강법을 수식화 한 것이다.
Algorithm

Learning Rate
경사하강법은 알고리즘상 반복적인 연산이 필요하다. 이동하는 간격(Step)이 너무 작으면 시간이 매우 오래 걸릴 수 있으므로 간격을 조정할 매커니즘이 필요한데 이때 사용되는 것이 Learning Rate 이다.
미분계수에 learning rate를 곱해줌으로써 learning rate가 작을수록 step이 작아지고, learning rate가 커질수록 step이 커지게끔 한다.
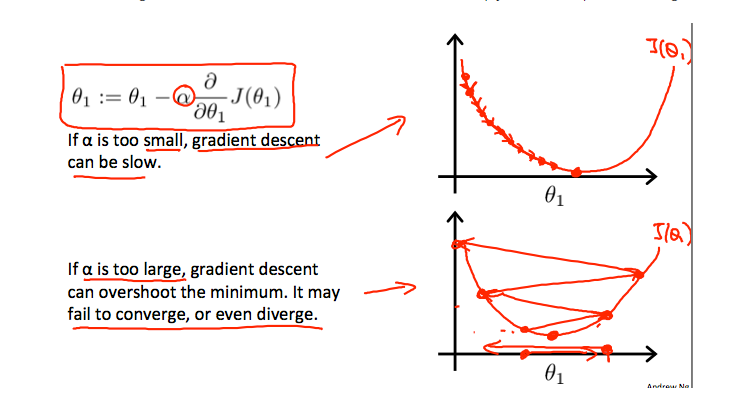
learning rate가 너무 작으면, 정확한 local optimum을 찾을 수는 있으나, 속도가 느려진다는 단점이 있고 learning rate가 너무 크면 local optimum에 도달하지 못하거나 다른 값을 찾게 되는 단점이 있으므로 learning rate를 적절히 설정하는 것이 필요하다.
'Information Technology > Machine Learning' 카테고리의 다른 글
| 로지스틱 회귀(Logistic Regression) (0) | 2021.01.25 |
|---|---|
| 다중 선형 회귀(Multiple Linear Regression) (0) | 2021.01.25 |
| 모델과 비용함수(Model and Cost Function) (0) | 2021.01.24 |
| 지도학습과 비지도학습 (0) | 2021.01.24 |