Heero

개요

이번 포스팅에서는 로지스틱 회귀에 대해 알아본다.

앞서 포스팅에서 소개했던 선형 회귀는 데이터의 구조를 선형으로 예측하는 모델이었으므로, 종속변수가 연속적인 값일 때 적용할 수 있는 모델이었다. 종속변수가 이산적일 때도 선형 회귀를 사용할 수 있을까?

아래의 사례를 살펴보자.

함수값 $\cfrac{1}{2}$ 기준으로 악성 여부를 판단하는 선형 모델이다. 현재의 데이터와 결과를 보면 잘 분류한 것으로 보인다.

그러나 다음의 그림을 보자.

데이터가 추가 되었고 데이터의 분포에 맞추어 모델이 수정되었다. 이때 함수값 $\cfrac{1}{2}$ 기준으로 분류하는 것은 적합하지 않아보인다. 이와 같이 새로운 데이터의 추가가 기존의 분류 모델에 큰 영향을 미치게 된다.

따라서 변량이 이산 데이터일 때 선형회귀 모델은 적합하지 않다. 이때 적용할 수 있는 모델이 바로 로지스틱 회귀 모델이다.

Logistic Regression

로지스틱 회귀 모델은 다음과 같은 구조를 띤다.

정의

로지스틱 회귀의 가설함수를 살펴보자. 시그모이드 함수라는 이름으로 잘 알려져 있다.

$$
h_\theta(x) = g(\theta^Tx)
$$
$$
z = \theta^Tx
$$
$$
g(z) = \cfrac{1}{1+e^{-z}}
$$

의미

$x$에 대하여 $f(x)$의 값이 $y$일 확률을 뜻한다.

다음이 성립한다.

$$h_\theta(x) = P(y=1|x;\theta) = 1 - P(y = 0 |x;\theta)$$
$$P(y = 0|x;\theta) + P(y = 1|x;\theta) = 1$$

※시그모이드 함수를 사용하는 이유

아래 블로그에 감동적일 정도로 매우매우 잘 설명되어 있다ㅠㅠ. 그래도 내 나름대로 다시 정리해보겠다.

(https://gentlej90.tistory.com/69)

위에서 보았듯기존의 회귀식은 좌변과 우변이 모두 연속형인 수를 가정하고 있다.

그런데 로지스틱 회귀에서 좌변(y)는 이산값이다.

우변값은 $-\infty$~$\infty$인데 좌변이 이산값이므로 등호를 만족할 수가 없다.

이에 좌변의 범위를 맞춰주는 작업을 하게 된다. 이때 사용하는 것이 Logit(Log + Odds) 변환이다.

Logit 변환은 오즈에 로그를 씌운 것이다.

오즈비는 어떠한 일이 일어날 확률을 일어나지 않을 확률로 나눈 것을 말하고 공식은 다음과 같다.

$$\cfrac{p(y=1|x)}{1-p(y=1|x)}$$

p(y=1|x)가 1에 가까워질수록 무한대에 수렴하고, 0이면 0이 되므로 오즈비는 (0, $\infty$) 의 범위를 가진다.

아직 우변이 음수의 범위를 가질 수도 있기 때문에 한번의 변환을 더 거쳐야 하는데 그것이 로그변환이다.

$$log(\cfrac{p(y=1|x)}{1-p(y=1|x)})$$

이제 우변과 동등한 (-$\infty$, $\infty$)의 범위를 갖게 되었다.

이제 x와 w파라미터를 통해 일반 회귀식으로 logit값을 예측할 수 있게 되었다. 그러나 우리는 logit값이 아닌 p값, 즉 1이 될 확률을 알고 싶은 것이다. 따라서 p에 대하여 식을 다시 정리한다.

$$log(\cfrac{p(y=1|x)}{1-p(y=1|x)}) = w_0 + w^Tx $$
$$\cfrac{p(y=1|x)}{1-p(y=1|x)} = e^{w_0 + w^Tx }$$
$$p(y=1|x)=e^{w_0 + w^Tx }({1-p(y=1|x)})$$
$$p(y=1|x) = e^{w_0 + w^Tx }-e^{w_0 + w^Tx }{p(y=1|x)}$$
$$p(y=1|x) + e^{w_0 + w^Tx }{p(y=1|x)} = e^{w_0 + w^Tx }$$
$$p(y=1|x)(1 + e^{w_0 + w^Tx }) = e^{w_0 + w^Tx }$$
$$p(y=1|x) = \cfrac{e^{w_0 + w^Tx }}{(1 + e^{w_0 + w^Tx })}$$
$$\cfrac{e^{w_0 + w^Tx }}{1 + e^{w_0 + w^Tx }} = \cfrac{1}{1+e^{-(w_0 + w^Tx)}}$$

logistic function이 도출되었다. 이제 회귀식의 값을 input으로 받아 0~1의 확률값을 반환하는 이 함수를 통해 확률을 구할 수 있게 되었다. 확률을 우리가 세운 기준점(cutoff값)과 비교하면 분류가 끝이 난다.

Logistic Regression의 비용함수

로지스틱 회귀의 비용함수는 선형회귀의 비용함수와 다른 함수를 사용한다.

선형회귀의 비용함수는 다음과 같았다.
$$J(\theta) = \cfrac{1}{m}\sum_{i=1}^m\cfrac{1}{2}(h_\theta(x^{(i)}) - y^{(i)})^2 $$

로지스틱 회귀의 가설함수는 비선형함수이기 때문에 이를 그대로 적용하면 $J(\theta)$가 볼록하지 않은(Non-Convex) 함수가 된다.

정의

로지스틱 회귀의 비용함수는 다음과 같다.

$$Cost(h_\theta(x), y) = -log(h_\theta(x)) if y=1$$
$$Cost(h_\theta(x), y) = -log(1-h_\theta(x)) if y=0$$

이 Cost함수는 크게 두 가지 특징을 가진다.

1. $y=1$일 때, $h_\theta(x)$가 1에 가까워질수록(가설이 정확할수록) cost가 0에 수렴하고, $h_\theta(x)$가 0에 가까워질수록 cost가 무한대로 수렴하는 특징을 가진다. $y=0$일 때는 반대로 $h_\theta(x)$가 0에 가까워질수록 cost가 0에 수렴하고, $h_\theta(x)$가 1에 가까워질수록 cost가 무한대로 수렴하는 특징을 가진다.
2. Cost함수가 선형이므로 비용함수 $J(\theta)도 볼록(Convex)한 함수임을 만족한다.

비용함수의 일반화

$$Cost(h_\theta(x), y) = -ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))$$
$$J(\theta) = -\cfrac{1}{m}\sum_{i=1}^m[-y^{(i)}log(h_\theta(x^{(i)})) -(1-y^{(i)})log(1-h_\theta(x^{(i)}))]$$

Logistic Regression에서 Gradient Descent

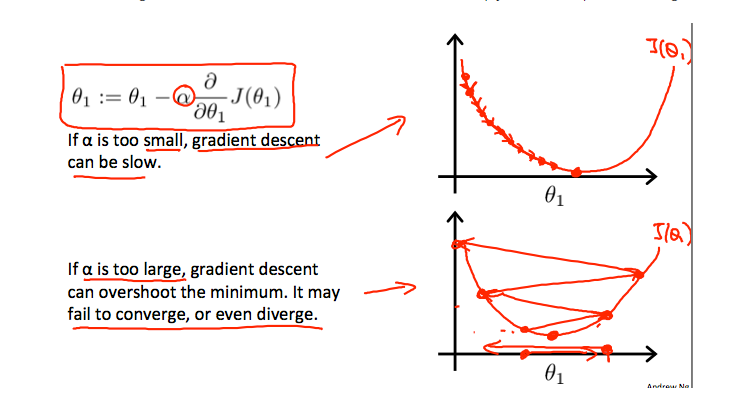
Gradient Descent는 아래의 식을 반복적으로 계산하여 수행한다.

$$\theta_j := \theta_j - \alpha\cfrac{\partial}{\partial\theta} J(\theta)$$

위에서 구한 $J(\theta)를 대입하면 다음의 식이 도출된다.

$$\theta_j := \theta_j - \cfrac{\alpha}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}$$

그런데 최종적인 형태는 선형 회귀의 Gradient Descent와 거의 같은 형태가 도출되었다.
차이점은 $h(x)$가 $\theta^TX$가 아닌 $ \cfrac{1}{1+e^{-\theta^Tx}}$ 라는 것이다.

이번 포스팅에 대해서는 다중 선형 회귀에 대해 알아보겠다. 먼저 선형 회귀에 대해 간단하게 알아보자.

선형회귀

앞선 포스팅에서 가설함수와 모델에 대해서 배웠었다. 모델은 쉽게 말하면 데이터의 구조에 대한 가정이라고 말했다.

선형 회귀도 모델의 일종인데, 모델이 하나의 선(line), 선형인 경우를 말한다. $ax+b$와 같은 일차함수가 대표적인 선형 회귀 모델이다.

다중 선형회귀

이때 $ax+b$는 독립변수가 1개이고, 종속변수도 1개인 단변량 단일 선형 회귀이다.

독립변수가 $x_1$, $x_2$ 등 2개 이상인 경우를 다중 선형 회귀라고 한다.

종속변수 1개, 독립변수 1개, => 단변량 단일 선형 회귀

종속변수 2개 이상, 독립변수 1개 => 다변량 단일 선형 회귀

종속변수 1개, 독립변수 2개 이상 => 단변량 다중 선형 회귀

종속변수, 독립변수가 모두 2개 이상 => 다변량 다중 선형 회귀

다중 선형회귀의 가설함수

단변량 다중 선형 회귀의 가설함수는 다음과 같이 벡터를 사용하여 표현할 수 있을 것이다.

다중 선형회귀의 비용함수

따라서 단변량 다중 선형 회귀의 비용함수는 다음과 같이 표현할 수 있다.

다중 선형회귀에서 경사하강법

앞서 경사하강법을 공부할 때 살펴본 단변량 단일 선형 회귀의 경우 경사하강법은 다음과 같이 적용했다.

각각의 파라미터는 다음의 과정을 거쳐 갱신되었다.

1. 비용함수를 각 파라미터 $\theta_0$, $\theta_1$ 에 대하여 편미분한다.

2. 각 계산된 미분계수와 learning rateα를 곱한 값을 $\theta_0$, $\theta_1$에서 빼준다.

3. 뺄셈한 결과값을 다시 $\theta_0$, $\theta_1$에 대입한다.

$\theta_0$, $\theta_1$의 경사하강법 공식은 언뜻보면 달라보이지만, 사실은 같은 모양이다. 아래의 그림을 참조하자.

$$
\theta_j := \theta_j - \alpha\cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}
$$

위의 $\theta_j$에 대하여 일반화한 공식을 그대로 적용한 것임을 알 수 있다. $\theta_0$의 경우 $x_0^{(1)}$을 곱하고 있는데, $x_0^{(1)}$이 벡터화 계산에서 $\theta_0$에 1을 곱해주려고 임의로 만들어낸 값이어서 생략되어 위의 형태를 띠게 된 것이다.

결론적으로 다중 선형회귀에서 경사하강법은 j=0부터 n까지에 대하여 경사하강법의 일반화 공식을 동시에 수행하는 것으로 정리될 수 있다. 

개요

전 포스팅에서 비용함수가 최소화될 때 최적의 파라미터를 찾을 수 있다고 서술했었다.

경사하강법은 미분을 이용하여 비용함수가 최소가 되는 지점을 기계가 자동으로 찾아낼 수 있도록 하는 방법이다.

개요는 다음과 같다.

1.  먼저 파라미터를 초기화 한다.
2.  J(θ0, θ1)에서 가장 경사진 지점으로 이동한다.
3.  이동한 지점의 θ0, θ1이 새로운 파라미터가 되고, 1,2의 과정을 반복한다.
4.  반복하면 국소 최적(Local Optimum)에 도달한다.

이때, 이동의 간격(step)을 지정할 수 있는데 이것을 learning rate, α라고 한다

어떻게 가장 경사진 지점으로 이동할 수 있을까?

그때 사용하는 것이 미분이다. 미분은 어떤 점에서의 기울기를 구할 때 사용한다. 어떤 점에서의 기울기에 비례해서 값을 감소시키면 경사진 지점으로 이동하게 된다. 비용함수에서 하강을 반복하다 보면 어느 순간 비용함수의 최저 지점에 도달할 수 있게 될 것이다.

최저지점에 도달할수록 기울기의 절대값이 작아지고, 하강하는 깊이도 점점 줄어든다. 따라서 비용함수가 일정수준 이상 감소하지 않는 지점을 국소 최적(local optimum)이라 판단하고 학습을 종료한다. 아래는 경사하강법을 수식화 한 것이다.

Algorithm

Learning Rate

경사하강법은 알고리즘상 반복적인 연산이 필요하다. 이동하는 간격(Step)이 너무 작으면 시간이 매우 오래 걸릴 수 있으므로 간격을 조정할 매커니즘이 필요한데 이때 사용되는 것이 Learning Rate 이다.
미분계수에 learning rate를 곱해줌으로써 learning rate가 작을수록 step이 작아지고, learning rate가 커질수록 step이 커지게끔 한다.

learning rate가 너무 작으면, 정확한 local optimum을 찾을 수는 있으나, 속도가 느려진다는 단점이 있고 learning rate가 너무 크면 local optimum에 도달하지 못하거나 다른 값을 찾게 되는 단점이 있으므로 learning rate를 적절히 설정하는 것이 필요하다.

모델이란

머신러닝은 주어진 학습 데이터셋에서 구조를 학습하고, 이후 데이터가 주어지면 학습한 구조를 바탕으로 예측을 수행하는 것이라고 말할 수 있다. 이때 '데이터가 어떤 구조를 가졌을 것이다'라는 가정을 모델이라고 한다.

모델을 정하고, 모델을 학습한 후, 실제 정답과의 오차를 바탕으로 모델을 평가하여 다시 수정하는 과정을 반복하면서 최적의 모델을 만들어 나가는 것이 머신러닝의 핵심이다.

이때 모델을 평가하는 과정에서 등장하는 개념이 비용함수(Cost Function) 이다

비용함수(Cost Function)

비용함수를 말하기 전에, 가설함수(Hypothesis Function)이라는 개념이 등장하는데, 가설함수는 어떤 데이터 X에 대하여 정답은 h(x)일 것이라고 예상하는 함수를 말한다. 모델과 유사한 개념이다.

h(x) = ax + b

h(x)를 위와 같이 가정했을 때 목표는 최적의 a와 b의 값을 찾아내는 것이다. 이때 어떤 최적의 a,b값은 h(x) - y(의 제곱)가 최소가 될 때 찾을 수 있을 것이다. 이때 a,b를 파라미터라고 부르고 파라미터는 θ로 표현한다.

비용함수는 어떤 h(x)에 대하여 실제 정답과 얼마나 큰 오차가 발생하는지(얼마나 예측이 정확한지)를 수치화하는 함수라고 할 수 있다. 최적의 모델은 비용함수가 최소화 되는 지점에서 찾을 수 있다. 비용함수는 J(θ)라고 표현한다.

비용함수의 일반화

앞으로 이어질 포스팅에서는 머신러닝의 거장 Andrew NG 스탠포드 교수가 Coursera라는 MOOC 플랫폼에서 진행하는 Machine Learning 강의를 기반으로 머신러닝에 대한 개략적인 내용을 서술하고자 한다. 총 11주 과정으로 구성되어 있지만 포스팅의 구성은 내가 중요하다고 생각하거나 관련있다고 생각하는 기준에 따라서 적절히 수정해서 구성할 것이다.

머신러닝이란?

• 컴퓨터가 프로그래밍 없이도 스스로 학습할 수 있는 능력을 가질 수 있도록 하는 연구
• 태스크(T)에 있어서 능률(P)을 경험(E)을 통해 향상시키고자 하는 연구
• E(Experience) + T(Task) + P(Probability)
• 머신러닝은 크게 두가지, 지도학습과 비지도학습으로 분류된다

지도학습(Supervised Learning)

주어진 데이터셋에 예측하고자 하는 정답이 명시적으로 포함된 경우를 말한다. 예를 들면 종양의 크기를 통해 유방암의 유무를 예측하고자 하는 경우, 집의 크기를 통해 집값을 예측하고자 하는 경우가 지도학습에 해당된다.

지도학습도 두 가지로 분류될 수 있는데, 회귀(Regression)과 분류(Classification)으로 나누어진다. 이에 대해서는 이어질 포스팅에서 서술한다.

비지도학습(Unsupervised Learning)

비지도학습에서는 데이터셋에 우리가 예측해야 할 정답이 명시적으로 포함되어 있지 않다. 학습을 통해 데이터셋에서 어떠한 구조를 찾아내는 것이 비지도학습의 궁극적 목표이다.